Calculating the orbit of a celestial body is critical in determining its characteristics and interactions with other objects in space. The sun itself orbits around the center of the Milky Way and completes a loop between 225 to 250 million years. You can also predict the position of planets and moons in their orbits, or determine where they were at any time in the past.
But how do we know that? By carefully measuring movements, it is possible to mathematically calculate the shape of the ellipses drawn by the orbits, something that astronomer Johannes Kepler discovered in the seventeenth century. Thanks to him, it only takes a few numbers to define the shape, size and spacial orientation of these ellipses.
Johannes Kepler was born in 1571 and was responsible for drafting the “Laws of Planetary Motion”, better known as the “Kepler Laws”. They describe basic characteristics of planetary motion: Solar System planets revolve around the Sun and describe approximately circular elliptical orbits; the speed of motion adapts to the position of the planet on the elliptic curve evenly, though not constantly, and there is a fixed ratio between the radius of the orbit and the time it takes the planet to describe it.
The planet for which there was the most data was Mars at that time. Kepler was able to study its orbit and determine the different positions of the earth after each sidereal period of Mars, and thus was able to trace the orbit of the earth. Still, he found that this orbit is in an eccentric circle, with the sun a little off center. Kepler was also able to determine the orbit of Mars.
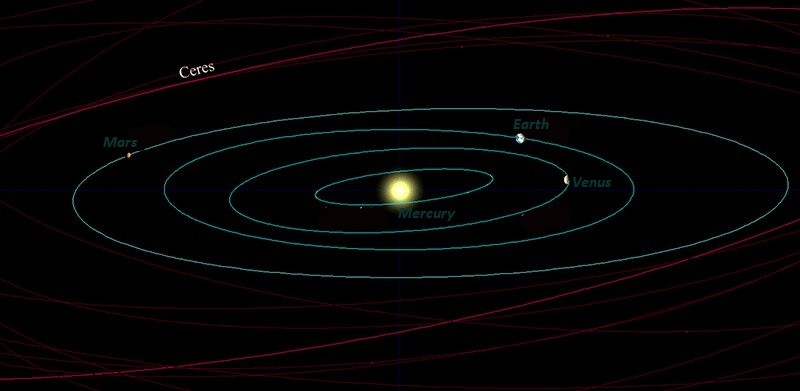
If you have some data and the location of the object in its orbit at any given time, you can use mathematical equations that deal with our problem – the movement of one body under the influence of the gravity of another body. Thus, it will be possible to predict where the object will be in the future and find out where it was in the past, which is essential for understanding the universe.
The more observations you make over time, the better you can define this ellipse, and the more confident you will be in determining the location of the object. And if you can get the numbers you need with sufficient precision, you may find that the object has been observed by another telescope in the past just by chance, having even more data for study.
You can then find a previous image of it and use it to further enlarge your observation data, further determining the numbers that define the ellipse. Astronomy benefits greatly from digital imaging because it is possible to save observations made to a database. Many asteroids and comets observed today were found in older images in this way.
It may sound simple, but it is not easy. The equations needed to do this can be daunting for novice advanced mathematics enthusiasts, and even astronomy students. Astronomer Phil Plait says that when he was an undergraduate, his homework consisted of a list of variables describing an asteroid’s orbital ellipse and a photo of a large area of the sky with “a bazillion stars,” as well as the asteroid itself, somewhere lost in the image.
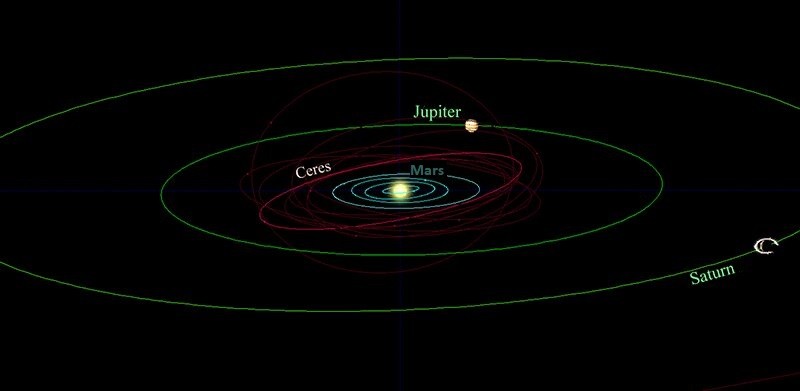
Given the sky coordinates of the center of the photograph and the date it was taken, the task was to find the asteroid. For this, it is necessary to apply equations to the given variables and work with mathematics. A ball not as exciting as looking at the sky with powerful telescopes, but indispensable for an astronomer, especially those of a time when there were no computers to do the most “boring” part of the job.
Ok, but how are the calculations made?
But how exactly is this done? What numbers are needed? Well, you’ll need something called orbital elements, or Kepler data, or keplerian data. Calculating the position of a planet was Kepler’s greatest work, hence the homage. These calculations are based on Kepler’s three laws, and Kepler’s data, a set of six parameters that allow the object’s orbit to be defined around any other celestial body.
Among these parameters, we have the length of the ellipse on its widest axis – the main axis. What we need for
the calculation is this value divided in half, called the main half axis. Another parameter is eccentricity, ie how far the ellipse is from a circle. Eccentricity values range from 0 to 1. An eccentricity of 0 is a perfect circle, and eccentricity 1 is no longer an ellipse, but a parable. The values of an ellipse can be 0.1, 0.5, 0.9, and so on.
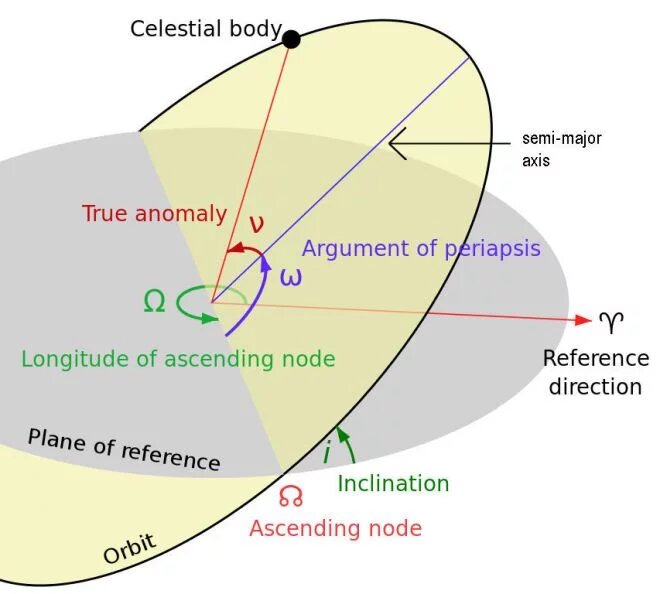
With the axis and the eccentricity, we already have the drawing of an ellipse. But there is still a long way to calculate an orbit. For example, to determine the orientation of this ellipse in space, you must define a reference plane, a kind of equator. The ellipse can then be slightly tilted to some degree. Let’s call this by the suggestive name “inclination.” The slope defines two points along the ellipse. At one point, the object is moving upwards relative to its reference plane, and at the other is moving downward. These are called ascending and descending points.
The orbital ellipse can also be rotated around its reference plane. Then you look at the angle between the rising point and some reference point in the sky (sometimes called the vernal point) and call it the longitude of the rising point. This angle tells you how much is rotated.
Then we have the so-called periapsy argument, which defines the orientation of the ellipse in the orbital plane. Periapsy is the nearest point at which the orbiting object arrives from the main object. Finally, we have the so-called true anomaly, which defines the position of the body in orbit along the ellipse at a specific time. Sometimes there are other parameters at play, but these are often the main ones.
If you have been able to follow this far, you can use these elements in equations that must be formulated correctly. The calculations themselves are easy with computers, so the really tricky part is getting Kepler’s orbital parameters. But if you can get them, just enter them into specific software codes and generate predictions of past and future object positions.
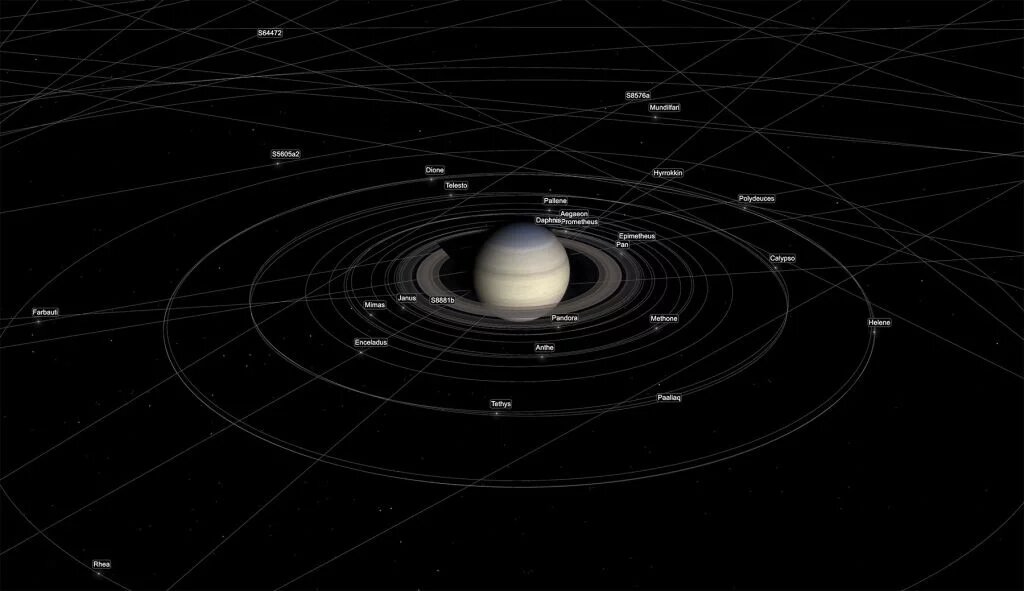
Recently 20 new moons were discovered around Saturn, and a few days later software engineer Ian Webster shared a page describing the orbits of these satellites in an animation. How was this possible? Well, the key is Keplerian orbital mechanics coupled with modern computing. If you have the equations programmed into a computer, all you have to do is add the orbital elements to the code.
You can also check out other orbit a
nimations like Jupiter’s moons and Jupiter’s orbit and other planets around the sun thanks to the work of the engineer mentioned above.
Source: Syfy
